In this blog, I would like to discuss a topic close to my heart: the intersection of ancient traditions and modern innovation. In India, Ayurveda is an ancient Indian health and wellness system that uses exercise, health, and medicine to heal the body and mind. Ayurvedic medicine originated in India over 3,000 years ago, and the term “Ayurveda” is derived from two Sanskrit words: Ayur (meaning life) and Veda (meaning knowledge or science), so Ayurveda translates to “the science of life.” Today, as we explore new ways to apply this wisdom, we combine traditional remedies with cutting-edge scientific techniques to create effective and safe modern medicines. 

The Ayurveda system emphasizes the balance between mind, body, and spirit, and some Ayurvedic remedies contain chiral compounds, which also include an element of balance or symmetry. Chiral compounds are molecules that are non-superimposable mirror images of each other, much like our left and right hands. Such molecules are central to the efficacy of specific medicines as only one enantiomer (hand) may provide the desired therapeutic effect, while its mirror image could be less effective or even harmful. This is why separating enantiomers is crucial in developing pharmaceutical products. 

One of the most modern and effective means of separating enantiomers is Supercritical Fluid Chromatography (SFC), an advanced technique well-suited to purifying enantiomers. By utilizing a chiral stationary phase, SFC can effectively differentiate and separate these mirror-image molecules. 

Utilizing another marriage of traditional knowledge and modern techniques, I shall explain how the Van Deemter equation can be used to optimize SFC, a technology that wasn’t available when Josef Van Deemter created his equation to maximize the efficiency of chromatographic separations.

How Can We Purify Enantiomers Using SFC?

Despite their similarity, enantiomers often have different biological activities, making their separation essential in many applications. Separating these mirror images is challenging due to their nearly identical properties—boiling point, melting point, and polarity. This is where SFC comes in. SFC is particularly effective for purifying enantiomers because the chiral stationary phase interacts differently with each enantiomer. This interaction can be compared to putting your hand in a glove—only one hand fits perfectly. Similarly, a chiral stationary phase differentiates enantiomers by forming diastereomeric interactions, leading to differences in their retention times.

The most used chiral stationary phases in SFC are modified polysaccharides, such as cellulose or amylose, which are coated or immobilized on silica gel. These polysaccharides have hydroxyl groups that form hydrogen bonds with the enantiomers. The spatial arrangement of these hydroxyl groups differs for each enantiomer, resulting in different interaction strengths. This difference in interaction allows one enantiomer to be retained more strongly in the column and thus become separated from its mirror image.

The beauty of using SFC for this purpose lies in its efficiency. Compared to High-Performance Liquid Chromatography (HPLC), SFC offers faster run times and reduced solvent consumption. This is because the mobile phase in SFC primarily comprises supercritical carbon dioxide (CO₂), which has a lower viscosity and higher diffusivity than the organic solvents used in HPLC. This allows for higher flow rates without sacrificing resolution. Additionally, CO₂ is much cheaper than the solvents typically used in HPLC, significantly reducing operational costs.

How Can We Optimize SFC Using the Van Deemter Equation

While SFC is a powerful tool for separating enantiomers, optimizing the process to achieve the best resolution and efficiency is vital. This is where the Van Deemter equation comes into play. The Van Deemter equation helps us understand how different factors contribute to band broadening during chromatographic separations. It allows us to fine-tune these parameters to minimize peak broadening and maximize resolution.

The equation is expressed as:

HETP = A + (B / u) + Cu

Where:

• HETP is the Height Equivalent to a Theoretical Plate.
• u is the linear velocity of the mobile phase.
• A, B, and C are the Van Deemter coefficients that correspond to:
• A – The multitude of paths the solute can take (“eddy diffusion”).
• B – The longitudinal diffusion of the solute.
• C – The mass transfer of the solute between the mobile and stationary phases.

We can optimize our chromatography method by understanding how each factor affects separation. For instance, Eddy diffusion (A) is minimized by using smaller particles in the stationary phase, reducing the variability in the molecules' paths through the column. Longitudinal diffusion (B) is most significant at low flow rates, so increasing the flow rate can help minimize its impact. However, if the flow rate is too high, mass transfer (C) becomes the limiting factor, as the analyte doesn’t have enough time to equilibrate between the mobile and stationary phases.

The Van Deemter equation is used to plot a curve showing the relationship between HETP and linear velocity (u). The curve typically has a U-shape, with the lowest point representing the optimal flow rate for maximum efficiency. This allows us to adjust the flow rate to find the sweet spot where separation is most efficient.

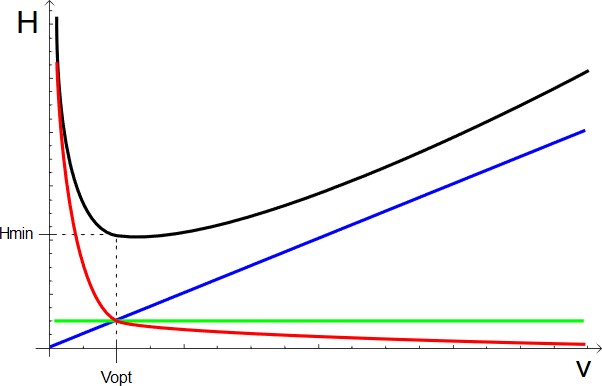
• Black line – HETP
• Blue line – Cu
• Green Line – A
• Red Line – B/u

How Can We Integrate SFC and the Van Deemter Equation for Optimal Enantiomer Separation?

In SFC, the choice of mobile phase and chiral stationary phase is crucial to purifying enantiomers. Optimizing the process involves balancing flow rate, column length, particle size, and pressure, and the Van Deemter equation guides us in adjusting these factors to achieve the highest resolution without compromising speed.

Supercritical carbon dioxide’s low viscosity and high diffusion coefficient allow for higher linear velocities than liquid solvents in HPLC. Supercritical fluids also penetrate packing material pores more efficiently, resulting in lower mass transfer diffusion values even for high linear velocities. This allows for shorter run times without loss of resolution, making SFC a more efficient and greener method due to the reduced solvent usage.

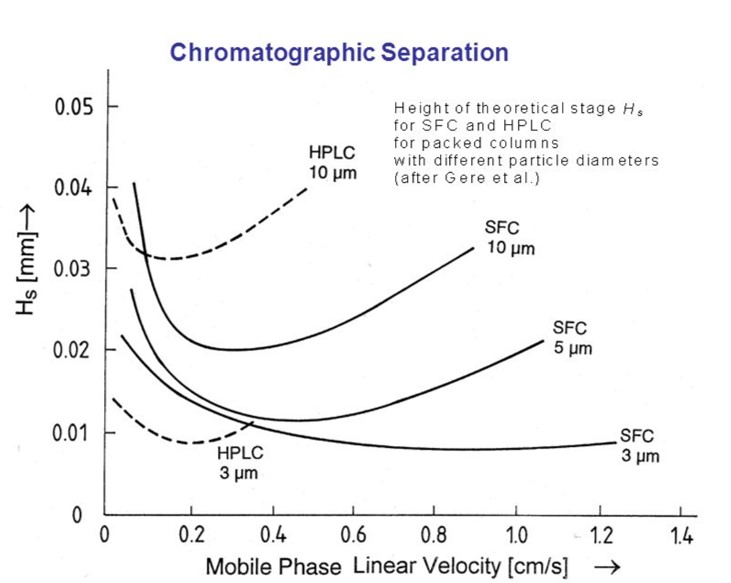
As you can see, the chosen method can significantly impact the speed and resolution of chromatographic separations.

The interplay of factors in SFC chromatography is complex. Still, by applying the Van Deemter equation, we can systematically optimize each parameter, ensuring that the purification of enantiomers is as efficient and precise as possible. So, whether you’re working in a pharmaceutical lab or an industrial setting, the combination of SFC and the Van Deemter equation can provide a powerful toolkit for tackling the challenges of enantiomer separation.

Phir Milenge Chalte Chalte,

Padma